Coordenadas Polares y Coordenadas Rectangulares. Las coordenadas polares y coordenadas rectangulares son sistemas utilizados para localizar puntos o objetos en una superficie.

Las coordenadas rectangulares se basan en ejes X e Y perpendiculares, mientras que las coordenadas polares consideran distancia y ángulo. En este artículo, exploraremos la conversión entre estos sistemas, incluyendo fórmulas y ejemplos prácticos.

Además, examinaremos la aplicación de estas coordenadas en navegación, geolocalización y cartografía. Descubre las ventajas y desventajas de cada sistema, y conoce más sobre estos sistemas de coordenadas.

Transformación de Coordenadas Polares a Coordenadas Rectangulares

En esta sección se aborda la transformación de coordenadas polares a coordenadas rectangulares, dos sistemas utilizados para representar la ubicación de puntos en el plano.

¿Qué son las Coordenadas Polares?

Las coordenadas polares son un sistema en el cual cada punto se describe mediante una distancia desde el origen y un ángulo desde un eje de referencia. La distancia se representa como "r" y el ángulo como "θ". Este sistema se utiliza para ubicar puntos en un círculo trigonométrico o en un plano polar.

¿Cómo se representan las Coordenadas Rectangulares?

Las coordenadas rectangulares, por otro lado, se basan en una representación mediante dos ejes perpendiculares: el eje X y el eje Y. El eje X se utiliza para medir el desplazamiento en dirección este-oeste, mientras que el eje Y mide el desplazamiento en dirección norte-sur. Un punto se ubica mediante su distancia desde el origen a lo largo de cada uno de estos ejes.

Fórmulas para Convertir Coordenadas Polares a Rectangulares

Para transformar coordenadas polares a coordenadas rectangulares, se utilizan las siguientes fórmulas:

• Coordenada X: X = r * cos(θ)
• Coordenada Y: Y = r * sin(θ)

Estas fórmulas permiten calcular las coordenadas rectangulares de un punto a partir de sus coordenadas polares. Se utiliza el valor de la distancia "r" y el ángulo "θ" para obtener las coordenadas X e Y correspondientes.

Ejemplos Prácticos de Conversión

Para ilustrar la conversión de coordenadas polares a rectangulares, se presentan ejemplos prácticos en los cuales se proporcionan las coordenadas polares de distintos puntos. Estos ejemplos muestran paso a paso cómo utilizar las fórmulas mencionadas anteriormente para obtener las coordenadas rectangulares correspondientes. Se destacan casos especiales y situaciones comunes que pueden surgir durante el proceso de conversión.

Método Alternativo para Transformar Coordenadas Polares a Rectangulares

En ocasiones, es posible que necesitemos convertir coordenadas polares a coordenadas rectangulares utilizando un método alternativo. En este caso, podemos hacer uso de los componentes X e Y en las coordenadas rectangulares y calcularlos mediante la trigonometría.

Esto también te interesa...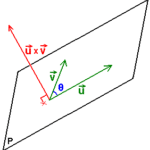Producto Cruz: Definición, cálculo y aplicaciones

Uso de Componentes X e Y en las Coordenadas Rectangulares

En las coordenadas rectangulares, el eje X representa la dirección Este-Oeste, mientras que el eje Y representa la dirección Norte-Sur. Estos componentes nos permiten determinar la posición exacta de un punto en un plano cartesiano.

Cálculo de los Componentes X e Y mediante Trigonometría

Para determinar los componentes X e Y de un punto a partir de las coordenadas polares, podemos utilizar cálculos trigonométricos. Dado un punto con una distancia r al origen y un ángulo θ con respecto al eje X, podemos utilizar las siguientes fórmulas:

• Componente X: X = r * cos(θ)
• Componente Y: Y = r * sin(θ)

Estas fórmulas nos permiten obtener las coordenadas rectangulares correspondientes a un punto dado en coordenadas polares. Al utilizar estos cálculos, es importante recordar que el ángulo debe estar en radianes para que las funciones trigonométricas trabajen correctamente.

Ventajas y Desventajas de los Sistemas de Coordenadas

Los sistemas de coordenadas, tanto rectangulares como polares, presentan ventajas y desventajas en su aplicación. A continuación, se detallan las principales características de ambos sistemas.

Precisión y Exactitud en Coordenadas Rectangulares

Las coordenadas rectangulares ofrecen una gran precisión y exactitud en la representación de puntos en un plano. Gracias a sus ejes perpendiculares, permiten una medición precisa de la distancia y ubicación de un punto en relación con el origen de coordenadas. Esto es especialmente útil en situaciones donde se busca un alto nivel de precisión, como en ingeniería o cartografía de detalle.

Ventajas de Utilizar Coordenadas Polares

Por otro lado, las coordenadas polares presentan ventajas en ciertos contextos de aplicación. Una de sus principales ventajas es la representación más intuitiva de direcciones y ángulos. Esto resulta especialmente útil en actividades como navegación marítima y aérea, donde es esencial la determinación precisa del rumbo. Además, las coordenadas polares simplifican la representación de formas circulares o curvas, como en el caso de secciones cónicas en matemáticas o en aplicaciones arquitectónicas.

Limitaciones y Consideraciones al Utilizar Coordenadas Polares

Sin embargo, las coordenadas polares presentan algunas limitaciones y consideraciones a tener en cuenta. Por ejemplo, en áreas cercanas al origen de coordenadas, la precisión puede verse comprometida debido a la reducción de la distancia medida. Además, la conversión de coordenadas polares a rectangulares puede requerir cálculos matemáticos adicionales y puede resultar más compleja en comparación con la conversión en sentido inverso. Por tanto, es importante evaluar cuidadosamente el contexto y las necesidades de cada situación antes de elegir el sistema de coordenadas más adecuado.

Ejemplos de Aplicación de Coordenadas Polares y Coordenadas Rectangulares

En esta sección, exploraremos diferentes aplicaciones prácticas de las coordenadas polares y rectangulares en diversos campos, mostrando su utilidad y ventajas en diferentes situaciones.

Navegación Marítima y Aérea utilizando Coordenadas Polares

En la navegación marítima y aérea, las coordenadas polares son fundamentales para determinar la posición y la ruta de una embarcación o aeronave. Mediante el uso de coordenadas polares, se pueden establecer puntos de referencia, calcular distancias y determinar la dirección de un objeto en relación con el origen de coordenadas. Los pilotos y navegantes utilizan brújulas y equipos de medición de distancia para obtener las coordenadas polares necesarias y así planificar sus trayectorias y evitar posibles obstáculos en su camino.

Aplicación de Coordenadas Rectangulares en Sistemas de Geolocalización

Los sistemas de geolocalización, como los utilizados en dispositivos GPS o en aplicaciones de mapas en teléfonos móviles, utilizan las coordenadas rectangulares para determinar la ubicación precisa en la superficie terrestre. Los sensores de estos dispositivos recopilan información sobre la posición relativa al origen de coordenadas y la representan en forma de coordenadas rectangulares. Estas coordenadas se pueden utilizar para encontrar direcciones, buscar lugares específicos y calcular distancias entre puntos en el mapa.

Esto también te interesa...Producto escalar de dos vectores: Cálculo y propiedades en Matemáticas

Coordenadas Polares en Mapeo y Cartografía

En el campo de la cartografía y el mapeo, las coordenadas polares son esenciales para representar características geográficas con precisión. Mediante la utilización de coordenadas polares, es posible ubicar y representar elementos como ríos, montañas, límites de regiones y puntos de interés en un mapa. Estas coordenadas permiten establecer relaciones espaciales entre diferentes áreas, facilitando la interpretación de la información geográfica y brindando referencias claras para la navegación.

Convertir Datos de GPS de Coordenadas Polares a Rectangulares

En ocasiones, es necesario convertir los datos de coordenadas polares proporcionados por dispositivos GPS a coordenadas rectangulares para su posterior análisis y representación. Esta conversión se realiza mediante fórmulas específicas que permiten traducir la distancia y el ángulo de las coordenadas polares en los valores correspondientes de coordenadas rectangulares X e Y. Este proceso es fundamental para utilizar los datos de localización en diferentes aplicaciones o para realizar análisis geoespaciales avanzados.

Dominando la Conversión de Coordenadas: De Rectangulares a Polares y el Fascinante Mundo del Producto Escalar

¿Listo para embarcarte en un emocionante viaje matemático? En este artículo, exploraremos el intrigante proceso de convertir coordenadas rectangulares en coordenadas polares. Pero eso no es todo; también descubriremos el sorprendente universo del producto escalar. ¡Prepárate para desentrañar estos conceptos matemáticos y llevar tus habilidades al siguiente nivel!

Coordenadas Rectangulares y Polares: Dos Formas de Ubicación Únicas

Imagina que estás en una gigantesca sala de juegos, y necesitas decirle a tus amigos exactamente dónde te encuentras. Las coordenadas son como tu mapa secreto. Ahora, tenemos dos maneras de dar esas coordenadas: rectangulares y polares.

Las coordenadas rectangulares son como dar direcciones en una cuadrícula. Imagina que el centro de la sala de juegos es el punto (0,0). Si te desplazas hacia la derecha, estás aumentando tu coordenada "x", y si te mueves hacia arriba, estás incrementando tu coordenada "y".

En cambio, las coordenadas polares son como decir cuánto debes caminar en cierta dirección y luego girar. Tienes dos partes en estas coordenadas: la distancia desde el punto central (llamémosla "r") y el ángulo que tienes que girar (llamémoslo "θ").

El Misterio de la Conversión: De Rectangulares a Polares

Ahora, aquí viene el truco emocionante: ¿cómo convertimos esas coordenadas rectangulares en coordenadas polares? ¡Vamos a resolver el enigma matemático!

Supongamos que tienes unas coordenadas rectangulares (x, y). Primero, calculamos la distancia "r" desde el origen utilizando el teorema de Pitágoras: r = √(x² + y²). Luego, para encontrar el ángulo "θ", usamos la función trigonométrica llamada tangente inversa (arco tangente): θ = arctan(y/x).

LA MAGIA DEL PRODUCTO ESCALAR REVELADA

Ahora, cambiemos de marcha y sumerjámonos en el mundo del producto escalar. Esto suena complicado, ¡pero en realidad es asombrosamente útil y comprensible!

Imagina que tienes dos vectores, que son como flechas con dirección y magnitud. El producto escalar es como medir cuán alineados están estos vectores. Si los vectores apuntan en la misma dirección, el producto escalar es grande. Si están en ángulos perpendiculares, el producto escalar es cero. Y si están en direcciones opuestas, el producto escalar es negativo.

Esto también te interesa...Media, mediana y moda: Medidas de tendencia central

CONQUISTANDO LA CONVERSIÓN Y EL PRODUCTO ESCALAR EN PROBLEMAS DEL MUNDO REAL

Ahora que hemos desentrañado los secretos de la conversión de coordenadas y el producto escalar, ¿cómo podemos aplicar este conocimiento en el mundo real? ¡Vamos a verlo!

Ejemplo 1: Navegación Eficiente

Imagina que eres un piloto en un avión y necesitas saber cuánto te desvías de tu ruta original. Utilizando coordenadas polares, puedes determinar la distancia y el ángulo con respecto a tu punto de partida. ¡Esto te ayuda a corregir tu rumbo rápidamente!

Ejemplo 2: Física en Acción

En física, el producto escalar es esencial. Puede ayudarte a calcular el trabajo realizado por una fuerza en una dirección particular. Por ejemplo, si empujas un objeto hacia arriba, el trabajo realizado es diferente de empujarlo hacia un lado.

Véase también

¿Cómo se relacionan las coordenadas polares y rectangulares?

Las coordenadas polares y coordenadas rectangulares son sistemas de referencia fundamentales en matemáticas y geometría. Estas dos representaciones están interconectadas a través de una estrecha relación que permite una comprensión más profunda de las formas en el espacio.

En las coordenadas polares, un punto se describe mediante su distancia radial (r) desde el origen y su ángulo polar (θ) respecto a un eje de referencia. Esta descripción puede ser convertida a coordenadas rectangulares (x, y) utilizando las fórmulas de conversión: x = r * cos(θ) y y = r * sin(θ). Aquí, r actúa como la hipotenusa del triángulo formado por las coordenadas rectangulares, y θ determina el ángulo entre la hipotenusa y el eje horizontal.

Esta relación entre sistemas de coordenadas es esencial para simplificar cálculos en diferentes contextos, desde ecuaciones paramétricas hasta la representación de curvas y regiones complejas. Además, las coordenadas polares a menudo resultan más convenientes para describir patrones circulares o radiales, mientras que las coordenadas rectangulares son ideales para representar movimientos y relaciones lineales.

En resumen, las coordenadas polares y rectangulares están estrechamente entrelazadas mediante su conversión matemática, brindando una manera poderosa de abordar problemas geométricos y algebraicos desde diversas perspectivas.

Coordenadas Cartesianas

Las coordenadas cartesianas son ampliamente utilizadas en matemáticas y física para representar puntos en un plano mediante los ejes X e Y. A diferencia de las coordenadas polares y rectangulares, las coordenadas cartesianas se basan en las distancias horizontales y verticales desde un punto de referencia. Este sistema de coordenadas es fundamental en el estudio de funciones y gráficas, permitiendo visualizar relaciones entre variables independientes y dependientes.

Esto también te interesa...Cómo identificar el grado de una ecuación: Guía práctica

Coordenadas Polares y Coordenadas Rectangulares en Matemáticas

Tanto las coordenadas polares como las rectangulares tienen una aplicación importante en el campo de las matemáticas. Las coordenadas polares se utilizan en ecuaciones y funciones polares, permitiendo representar curvas como las circunferencias, elipses y espirales. Por otro lado, las coordenadas rectangulares son fundamentales para el estudio de álgebra lineal y geometría analítica, facilitando la representación de líneas rectas y figuras geométricas en el plano cartesiano.

Comparativa de Sistemas de Coordenadas

Comparar los sistemas de coordenadas es esencial para comprender sus diferencias y aplicaciones en diversos campos. Las coordenadas cartesianas ofrecen una representación simplificada de la posición de un punto, facilitando la manipulación matemática. Por otro lado, las coordenadas polares permiten una descripción más intuitiva en situaciones donde la distancia y el ángulo son relevantes, como en navegación marítima o astronomía.

El Camino Hacia la Maestría Matemática

Espero que hayas disfrutado explorando las coordenadas rectangulares y polares, así como el fascinante mundo del producto escalar. Estos conceptos no solo son poderosos en el ámbito matemático, sino que también tienen aplicaciones en la vida real.

Recuerda, las matemáticas son como una aventura continua. Cuanto más profundices, más maravillas descubrirás. Así que, ya sea que estés en el primer nivel de tu viaje matemático o estés listo para avanzar, ¡siempre hay más por aprender y explorar!

Entonces, ¿estás listo para enfrentar nuevos desafíos matemáticos y aprovechar al máximo las coordenadas y el producto escalar? ¡Adelante, conquista el mundo matemático con confianza!

Uso de las coordenadas polares para casos reales

Las coordenadas polares se utilizan en muchos casos reales en los que es más conveniente describir la posición de un punto en términos de su distancia y ángulo con respecto a un punto de referencia. Esta representación es especialmente útil en problemas de navegación, como la localización de barcos en el océano o la determinación de la posición de un avión en el aire. Las coordenadas polares permiten una descripción más intuitiva y precisa de la posición de estos objetos en relación con un punto de referencia fijo.

Otro ejemplo de uso de las coordenadas polares se encuentra en el análisis de fenómenos periódicos, como las ondas y las señales. En estos casos, la amplitud y la fase de la señal se pueden describir de manera más sencilla utilizando coordenadas polares. Además, las coordenadas polares son ampliamente utilizadas en campos como la física y la ingeniería, especialmente en el estudio de sistemas con simetría circular, como el movimiento de planetas alrededor del sol o el análisis de antenas.

En el ámbito de la navegación, las coordenadas polares también se utilizan para la navegación marítima y la cartografía. Los navegantes pueden utilizar las coordenadas polares para determinar su posición exacta en el océano en relación con puntos de referencia conocidos, como faros o boyas. Además, los cartógrafos utilizan las coordenadas polares para representar la superficie de la Tierra en mapas y planos, lo que permite una representación más precisa y detallada del mundo que nos rodea.

Por último, las coordenadas polares también son útiles en campos como la robótica y la visión por computadora. En estos casos, las coordenadas polares se utilizan para describir la posición y orientación de objetos en un espacio tridimensional, lo que es esencial para la planificación de movimientos y la detección de objetos en entornos complejos. Las coordenadas polares permiten una representación más natural y fácil de entender de la posición de los objetos en relación con un punto de referencia.

¿Tienes dudas o necesitas asesoría?

Con gusto te ayudamos en este y otros temas de matemáticas. Puedes contratar tu sesión de Regularización académica o escribe tu pregunta en la sección de comentarios al final de esta página sobre los temas en que necesitas ayuda. Este soy yo.

Esto también te interesa...Números complejos: Su impacto en la vida diaria y aplicaciones prácticas

Aprende a convertir coordenadas polares a rectangulares con ejercicios resueltos y práctica guiada.

---

Si quieres conocer otros artículos parecidos a Coordenadas Polares y Coordenadas Rectangulares: Ejemplos y Conversión puedes visitar la categoría Matemáticas.