Expresión algebraica. Aprende sobre las combinaciones de letras y números

Expresión Algebráica, ¿Qué es? ¿Cuál es su definición?. Las expresiones algebraicas son combinaciones de letras y números unidos por operaciones matemáticas básicas como la suma, la resta, la multiplicación y la división.

Son muy útiles para resolver problemas en matemáticas y en la vida diaria. En este artículo vamos a aprender qué son las expresiones algebraicas, cómo se componen, sus diferentes tipos, y cómo realizar operaciones con ellas para obtener el resultado. También veremos cómo calcular su valor numérico y cuál es su importancia en la matemática y la vida cotidiana.

Qué son las expresiones algebraicas

Para entender las expresiones alegbráicas primero debemos saber que el álgebra es combinación de letras y números ligadas por los signos de las operaciones básicas.En el sistema de numeración y operaciones aritméticas, existe un concepto que describe la combinación de números y letras relacionados mediante operaciones. Este concepto se conoce como álgebra.

El álgebra es una rama de las matemáticas que se encarga de estudiar las propiedades y las reglas que rigen los números y las operaciones, tanto numéricas como algebraicas. En el álgebra, las letras son utilizadas para representar números desconocidos o variables, y se pueden combinar con números conocidos para formar expresiones algebraicas.

A través de las operaciones aritméticas de suma, resta, multiplicación y división, es posible simplificar y resolver dichas expresiones para encontrar valores específicos. De esta manera, el álgebra proporciona herramientas para resolver problemas y modelar situaciones del mundo real utilizando una combinación de números y letras.

Ahora sí podemos responder a la pregunta ¿Cuál es el concepto que describe la combinación de números y letras relacionados mediante operaciones aritméticas? Este concepto es el álgebra.

Desde la definición del álgebra estamos listos para definir las expresiones algebráicas y su utilidad.

Definición de expresión algebraica

Según la definición de las expresiones algebraicas, se trata de una combinación de variables, coeficientes y operadores matemáticos, que permiten ejecutar diferentes operaciones matemáticas. Esta combinación puede contener solo números o solo letras, aunque lo más común es que contengan ambas.

Partes de una expresión algebraica

Polinomios

Los polinomios son un tipo de expresión algebraica que se compone por términos compuestos por variables, coeficientes y exponentes. Los polinomios pueden tener diferentes grados, y se pueden representar en forma de suma o resta de términos.

Parte numérica

La parte numérica de una expresión algebraica es la que se compone por números, y que se relaciona mediante operaciones aritméticas básicas, como la suma, la resta, la multiplicación y la división. Esta parte es importante para el cálculo del valor numérico de una expresión algebraica.

Parte literal

La parte literal de una expresión algebraica es la que se compone por variables, es decir, letras que representan números. Estas variables pueden estar acompañadas por exponentes literales, y son importantes en el cálculo del valor numérico de una expresión algebraica.

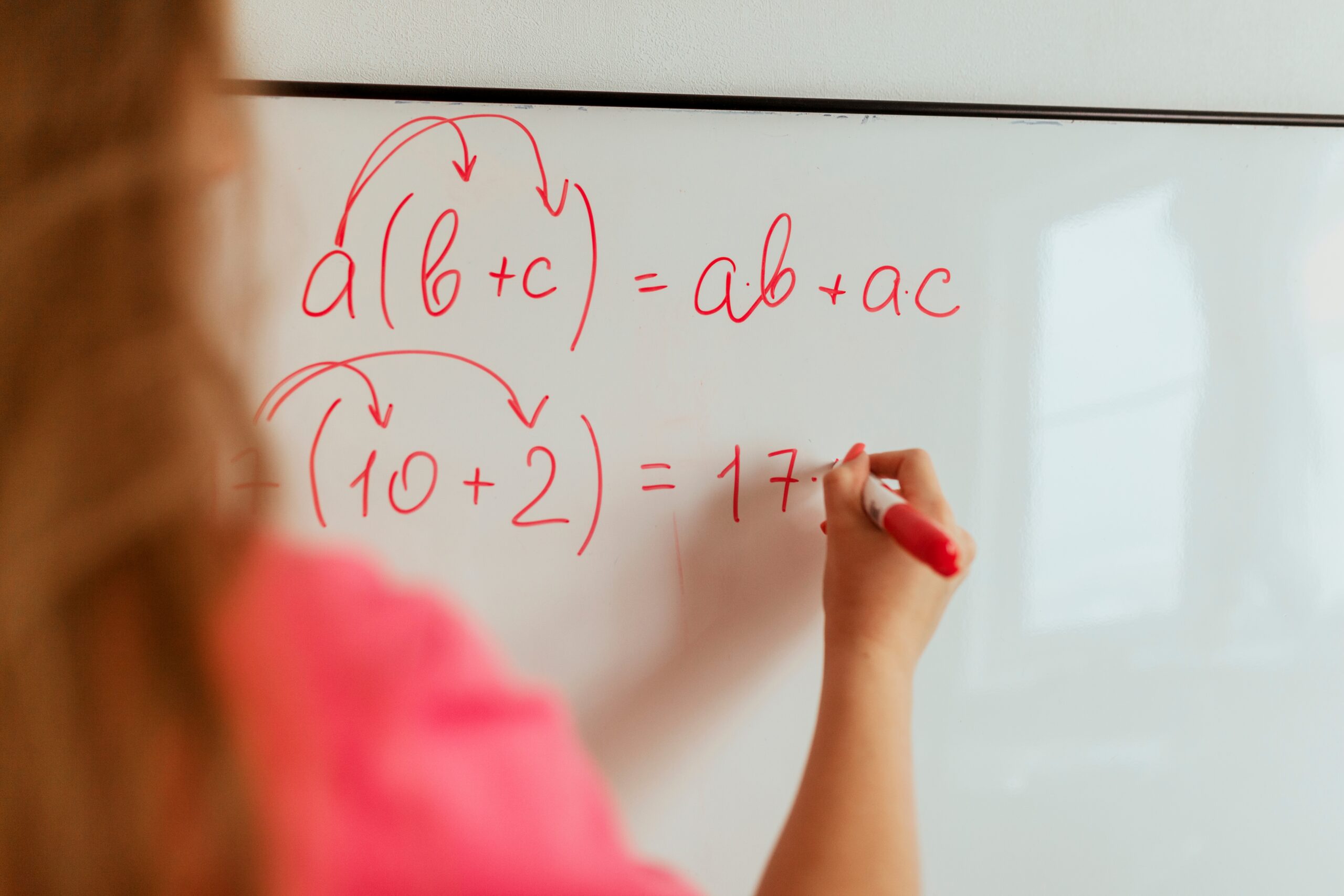
Ejemplos de expresiones algebraicas

Algunos ejemplos de expresiones algebraicas son:

Esto también te interesa...Introducción al cálculo diferencial y sus aplicaciones: todo lo que necesitas saber

• 2x + 5y
• 3x² - 2x + 1
• 4a³ + 2b² - 7c + 2

Como se puede observar, en estas expresiones algebraicas se combinan tanto variables como coeficientes, que se relacionan mediante diferentes operaciones matemáticas.

Operaciones con expresiones algebraicas

Las expresiones algebraicas se utilizan para resolver problemas matemáticos, y es esencial conocer las operaciones básicas que se pueden realizar con ellas. En esta sección se explican cómo llevar a cabo las operaciones de suma, resta, multiplicación y división, así como la simplificación de fracciones algebraicas.

Suma y resta de expresiones algebraicas

La suma y la resta de expresiones algebraicas se realizan combinando términos semejantes. Los términos semejantes son aquellos que tienen las mismas variables con los mismos exponentes. Para realizar estas operaciones, se deben seguir las reglas de signos:

• Si los términos son iguales, se suman sus coeficientes y se deja la misma variable y el mismo exponente.
• Si los términos tienen signos opuestos, se restan sus coeficientes y se deja la misma variable y el mismo exponente.

Multiplicación de expresiones algebraicas

La multiplicación de expresiones algebraicas se realiza utilizando la propiedad distributiva. Para multiplicar dos polinomios, se multiplican todos los términos del primer polinomio por todos los términos del segundo polinomio.

• Para multiplicar dos monomios, se multiplican sus coeficientes y se suman los exponentes de las variables.
• Para multiplicar un polinomio por un monomio, se multiplica cada término del polinomio por el monomio y se suman los resultados.

División de expresiones algebraicas

La división de expresiones algebraicas se utiliza para simplificar una expresión compleja en términos más sencillos. Se puede utilizar la división algebraica o la regla de Ruffini para dividir polinomios.

• La división algebraica se realiza mediante una técnica similar a la división aritmética.
• La regla de Ruffini, también llamada división sintética, se utiliza para dividir un polinomio de grado n entre un binomio de la forma (x - a), donde a es una constante.

Fracciones algebraicas

Las fracciones algebraicas se utilizan para representar divisiones de expresiones algebraicas. Para simplificar fracciones algebraicas, se deben seguir las reglas de simplificación de fracciones comunes, como reducir términos semejantes y factorizar términos similares.

• Para sumar o restar fracciones algebraicas, se deben encontrar el común denominador y realizar la operación sobre los numeradores.
• Para multiplicar fracciones algebraicas, se multiplican los numeradores y los denominadores.
• Para dividir fracciones algebraicas, se multiplican la primera fracción por la inversa de la segunda.

Valor numérico de una expresión algebraica

El valor numérico de una expresión algebraica es el resultado que se obtiene al sustituir las variables por números. Es importante conocer el valor numérico de una expresión algebraica porque permite evaluarla y resolver problemas matemáticos y en la vida cotidiana.

Para resolverla se acostumbra colocar los números en la expresión algebraica a la derecha del signo y efectuar las operaciones aritméticas que resulten.

Cálculo del valor numérico

El cálculo del valor numérico se realiza al sustituir las variables por números, respetando las operaciones matemáticas. Primero, se realizan las operaciones dentro de los paréntesis, luego los exponentes, seguido de la multiplicación y división de izquierda a derecha y, finalmente, la suma y resta de izquierda a derecha.

Sustitución de valores

Para calcular el valor numérico de una expresión algebraica se deben seguir los siguientes pasos:

• Identificar la variable o variables a sustituir por los valores numéricos correspondientes.
• Sustituir cada variable por el valor numérico correspondiente.
• Realizar las operaciones matemáticas siguiendo el orden adecuado para obtener el resultado final.

Ejemplos de cálculo del valor numérico

A continuación, se presentan algunos ejemplos de cómo calcular el valor numérico de una expresión algebraica:

• Para la expresión algebraica 5x + 2, si se sustituye x por 3, el valor numérico será 17.
• Para la expresión algebraica 2x^2 + 3x + 1, si se sustituyen x por 2, el valor numérico será 13.
• Para la expresión algebraica (3x + 2)(2x - 1), si se sustituye x por 4, el valor numérico será 50.

Es importante tener en cuenta que el valor numérico puede ser diferente según los valores que se elijan para las variables. Por esta razón, es esencial verificar que los valores numéricos utilizados sean los correctos y estén en concordancia con lo que se está evaluando.

Grado y coeficiente principal de un polinomio

En álgebra, un polinomio es una expresión algebraica que contiene términos combinados por los operadores matemáticos básicos de suma, resta, multiplicación y división. Cada término de un polinomio está compuesto por una parte numérica y una parte literal. La parte literal incluye una letra que representa la variable y un exponente que indica su grado.

Definición de grado y coeficiente principal

El grado de un polinomio se refiere a la máxima potencia de la variable presente en el polinomio. Por ejemplo, en el polinomio 3x^4+ 2x^3-5x+1, la máxima potencia de la variable x es 4, por lo tanto, el grado del polinomio es 4.

El coeficiente principal, en cambio, es el coeficiente que acompaña al término con el grado más alto del polinomio. Es decir, si tenemos el polinomio 4x^3+5x^2+3x+2, el coeficiente principal es 4.

Esto también te interesa...Entendiendo las Medidas de Tendencia Central: Definición y Explicación

Cálculo del grado de un polinomio

Para calcular el grado de un polinomio, es necesario identificar el término con la máxima potencia de la variable. De esta manera, para el polinomio 2x^3+5x^2-4x+1, el término con la máxima potencia de la variable es 2x^3, por lo que el grado del polinomio es 3.

En el caso de los polinomios con varios términos, es importante verificar que todos los términos tienen la misma variable y la misma base del exponente. En caso contrario, el polinomio no se puede simplificar a grado único.

Cálculo del coeficiente principal

Para calcular el coeficiente principal, se identifica el término con el grado más alto del polinomio y se extrae el coeficiente que lo acompaña. En el polinomio 3x^4+2x^3+5x^2+6, el término con el grado más alto es 3x^4 y su coeficiente es 3. Por lo tanto, el coeficiente principal del polinomio es 3.

Para los polinomios con exponentes negativos, el coeficiente se extrae en la misma forma, pero se cambia el signo del exponente.

• El grado de un polinomio siempre es un número natural o cero.
• En un polinomio constante, el grado es cero.
• En un polinomio con un solo término, se debe revisar la base del exponente para verificar si se trata de un monomio, binomio o trinomio.

¿Cuál es la utilidad de la expresión algebraica dentro de las operaciones matemáticas?

La expresión algebraica es una herramienta fundamental en las operaciones matemáticas. A través de la utilización de letras y números, la expresión algebraica nos permite generalizar y representar situaciones matemáticas de forma más flexible y abstracta. Su utilidad radica en que nos permite simplificar y resolver problemas matemáticos de manera más eficiente, así como establecer relaciones y patrones entre diferentes cantidades o variables.

• Nos permite generalizar situaciones matemáticas y representarlas de forma más flexible y abstracta.
• Simplifica la resolución de problemas matemáticos, al permitirnos trabajar con fórmulas y ecuaciones.
• Establece relaciones y patrones entre diferentes cantidades o variables.
• Facilita la comunicación matemática al utilizar símbolos y notaciones comunes.
• Permite modelar y resolver problemas en diversas áreas como física, economía, ingeniería, entre otras.

Ejercicios resueltos de expresiones algebraicas

En esta sección se presentan ejercicios resueltos para reforzar el aprendizaje de las operaciones básicas con expresiones algebraicas. Es importante recordar que para resolver correctamente los ejercicios se deben tener claros los conceptos básicos de cada operación.

En matemáticas, sustituir los valores de las variables en una expresión algebraica es un proceso fundamental para encontrar resultados específicos. Esto se hace al reemplazar las incógnitas o variables en la expresión con números o valores conocidos.

Por ejemplo, si tenemos la expresión algebraica 3x + 2y - z, y se nos proporcionan los valores x = 4, y = 5 y z = 2, podemos sustituir estos valores en la expresión para obtener 3(4) + 2(5) - 2.

Al calcular esta expresión, obtenemos el resultado de 22.

Sustituir los valores de las variables en una expresión algebraica nos permite simplificarla y encontrar soluciones precisas a problemas matemáticos.

Ejercicios de suma y resta de expresiones algebraicas

En este tipo de operaciones algebraicas, se deben juntar o separar términos semejantes, es decir, aquellos que tienen las mismas letras elevadas a los mismos exponentes. A continuación, se presentan ejemplos de suma y resta de expresiones algebraicas:

• 3x + 4y + 2x - 5y = (3+2)x + (4-5)y = 5x - y
• 5ab - 2cd - 3ab + cd = (5-3)ab + (-2+1)cd = 2ab - cd

Ejercicios de multiplicación de expresiones algebraicas

En este tipo de operaciones, se deben aplicar las propiedades distributivas para multiplicar cada término de una expresión por todos los términos de otra. A continuación, se presentan ejemplos de multiplicación de expresiones algebraicas:

• (4x + 2)(3x - 1) = 4x(3x-1) + 2(3x-1) = 12x² - 2x - 2
• (5a - 2b)(2a + 3b) = 5a(2a+3b) - 2b(2a+3b) = 10a² + 15ab - 4ab - 6b² = 10a² + 11ab - 6b²

Ejercicios de división de expresiones algebraicas

En este tipo de operaciones, se deben realizar las operaciones de división algebraica, teniendo en cuenta las reglas establecidas para cada caso. A continuación, se presentan ejemplos de división de expresiones algebraicas:

• (6x² + 5x - 1) ÷ (2x + 1) = 3x - 1
• (4a³ + 2a²b - 4a²c - 2ab² + bc) ÷ (2a + b) = 2a² - 2ac + b

Ejercicios de valor numérico de expresiones algebraicas

Para calcular el valor numérico de una expresión algebraica, se deben reemplazar las letras por los valores numéricos correspondientes y realizar las operaciones indicadas. A continuación, se presentan ejemplos de cálculo del valor numérico de expresiones algebraicas:

• Si x = 2, entonces 3x² - 2x + 1 = 3(2)² - 2(2) + 1 = 11
• Si a = 3 y b = 2, entonces 4a - 2b + ab = 4(3) - 2(2) + 3(2) = 14

Ejercicios de grado y coeficiente principal de polinomios

El grado de un polinomio se refiere al exponente más alto que tiene una variable en el polinomio. El coeficiente principal de un polinomio es el coeficiente del término de mayor grado. A continuación, se presentan ejercicios de cálculo del grado y coeficiente principal de polinomios:

Esto también te interesa...Números romanos: Guía completa para entender y utilizarlos

• Si f(x) = 2x³ + 5x² - 3x + 2, entonces el grado de f(x) es 3 y el coeficiente principal es 2.
• Si g(x) = 4x² - 6x + 1, entonces el grado de g(x) es 2 y el coeficiente principal es 4.

Definiciones y operaciones de expresiones algebraicas

• Las expresiones algebraicas son combinaciones de letras y números relacionadas mediante operaciones matemáticas como sumas, restas, multiplicaciones y divisiones.
• Las expresiones algebraicas se dividen en polinomios, que a su vez tienen parte numérica y parte literal.
• Para operar con expresiones algebraicas se usan reglas específicas para cada tipo de operación.

Valor numérico de una expresión algebraica

• Calcular el valor numérico de una expresión consiste en sustituir las variables por valores concretos y simplificar la expresión resultante.
• Para calcular el valor numérico de una expresión algebraica se recomienda utilizar una variable para sustituir el valor a calcular.

Grado y coeficiente principal de un polinomio

• El grado de un polinomio es la suma de los exponentes de sus términos de mayor grado.
• El coeficiente principal de un polinomio es el coeficiente del término de mayor grado.
• El cálculo del grado y coeficiente principal depende del tipo de polinomio del que se trate.

Ejercicios resueltos de expresiones algebraicas

• Se presentan ejercicios resueltos para cada tipo de operación con expresiones algebraicas y para el cálculo de valor numérico y grado y coeficiente principal de un polinomio.

Importancia de las expresiones algebraicas en las matemáticas y la vida cotidiana

En matemáticas

• Las expresiones algebraicas son fundamentales para la resolución de ecuaciones y la manipulación de las fórmulas matemáticas de forma general.
• El álgebra es una herramienta necesaria en la mayoría de las ramas de la matemática, desde la geometría hasta el cálculo.
• El conocimiento y manejo de las expresiones algebraicas resulta esencial para el aprendizaje de las matemáticas avanzadas.

En la vida cotidiana

• Las expresiones algebraicas se utilizan de forma cotidiana en cuestiones como el cálculo de intereses bancarios o de impuestos.
• La resolución de problemas cotidianos en el hogar o en el trabajo, como el cálculo de cantidades de materiales o la determinación de precios, suelen requerir el uso de expresiones algebraicas.
• El álgebra es útil en la toma de decisiones y la resolución de problemas en numerosos campos, desde la ingeniería hasta la economía.

La utilidad de la expresión algebraica dentro de las operaciones matemáticas es amplia y fundamental para resolver problemas y representar relaciones matemáticas. La expresión algebraica es una combinación de números, operadores y símbolos de variable, que permite generalizar fórmulas y ecuaciones para trabajar con valores desconocidos.

Al utilizar expresiones algebraicas, es posible simplificar cálculos complejos, resolver ecuaciones y representar relaciones matemáticas de manera generalizada. Además, las expresiones algebraicas permiten modelar situaciones reales y describir fenómenos mediante el uso de variables que pueden tomar diferentes valores.

En resumen, la utilidad de la expresión algebraica dentro de las operaciones matemáticas radica en su capacidad de simplificar cálculos, resolver problemas y representar relaciones matemáticas de manera generalizada.

Regla de signos en la suma y resta

Regla de signos en la suma y resta. La regla de signos en la suma y resta es una herramienta fundamental en la resolución de operaciones matemáticas que involucran números positivos y negativos. Esta regla nos permite determinar el signo del resultado de una suma o resta, facilitando así la simplificación y comprensión de los cálculos.

En términos generales, la regla establece que cuando se suman o restan números con el mismo signo, el resultado será un número con el mismo signo. Por ejemplo, si tenemos dos números positivos y los sumamos, el resultado será también positivo. Por otro lado, si los números tienen signos opuestos, la regla indica que el resultado tendrá el signo del número de mayor valor absoluto. Por ejemplo, si restamos un número positivo de uno negativo, el resultado será negativo si el número positivo tiene un valor absoluto mayor que el número negativo.

Regla de signos en la suma y resta: concepto y aplicaciones

La regla de signos en la suma y resta es un concepto fundamental en matemáticas que nos permite determinar el signo de un resultado al sumar o restar números. Esta regla establece que si dos números tienen el mismo signo (positivo o negativo), su suma o resta será también positiva. Por otro lado, si los números tienen signos opuestos, el resultado será negativo.

Esta regla tiene aplicaciones prácticas en diversas áreas como la física, la química y la economía. En física, por ejemplo, se utiliza para determinar la dirección y magnitud de la velocidad de un objeto en movimiento. En química, se aplica para balancear ecuaciones químicas y calcular la cantidad de sustancias involucradas en una reacción. En el ámbito económico, la regla de signos es esencial para realizar operaciones financieras como sumas y restas de ingresos y gastos.

Otro aspecto importante de la regla de signos es su relación con los números positivos y negativos en la recta numérica. Los números positivos se representan a la derecha del cero y los negativos a la izquierda. Al sumar o restar números, podemos visualizar el resultado como un desplazamiento a la derecha (si es positivo) o a la izquierda (si es negativo) en la recta numérica.

En resumen, la regla de signos en la suma y resta nos permite determinar el signo de un resultado al operar con números. Su aplicación práctica abarca diferentes disciplinas, desde la física hasta la economía. Además, esta regla está relacionada con la representación gráfica de los números positivos y negativos en la recta numérica.

Importancia de la regla de signos en las operaciones aritméticas

La regla de signos es fundamental en las operaciones aritméticas. Esta regla nos permite determinar el signo de un resultado en función de los signos de los números involucrados en la operación. Es una herramienta básica que facilita y agiliza los cálculos matemáticos.

En la suma y resta, la regla de signos nos indica que si los números tienen el mismo signo, se suman o restan y el resultado tendrá el mismo signo. Por ejemplo, si tenemos dos números negativos, al sumarlos obtendremos un resultado negativo. Si los números tienen signos diferentes, se restan y el resultado tomará el signo del número de mayor valor absoluto. Por ejemplo, si restamos un número positivo de uno negativo, el resultado será negativo.

Esta regla es especialmente útil al resolver problemas que involucran cambios de signo. Por ejemplo, al calcular el cambio de temperatura entre dos días, si el primer día hace más frío que el segundo, el resultado será negativo, indicando una disminución de temperatura. Si el primer día hace más calor que el segundo, el resultado será positivo, indicando un aumento de temperatura.

En la multiplicación y división, la regla de signos establece que si los números tienen el mismo signo, el resultado será positivo. Por ejemplo, si multiplicamos dos números positivos, obtendremos un resultado positivo. Si los números tienen signos diferentes, el resultado será negativo. Por ejemplo, si multiplicamos un número positivo por uno negativo, el resultado será negativo.

En resumen, la regla de signos es esencial para realizar operaciones aritméticas de manera correcta y eficiente. Nos permite determinar el signo de los resultados y facilita la resolución de problemas que involucran cambios de signo. Es una herramienta básica que todo estudiante de matemáticas debe dominar para tener éxito en sus cálculos.

Ejemplos prácticos de la regla de signos en la suma y resta

La regla de signos en la suma y resta es un concepto fundamental en matemáticas que nos permite determinar el signo resultante al sumar o restar números con distintos signos. Esta regla establece que si los números tienen el mismo signo, el resultado de la operación será positivo. Por otro lado, si los números tienen signos opuestos, el resultado será negativo.

Esto también te interesa...Coordenadas Polares y Coordenadas Rectangulares: Ejemplos y Conversión

Para entender mejor esta regla, consideremos el siguiente ejemplo: si sumamos -3 + (-7), ambos números tienen el mismo signo negativo, por lo que el resultado será positivo. Por lo tanto, -3 + (-7) = -10.

Por otro lado, si tenemos la expresión -8 - 4, los números tienen signos opuestos. De acuerdo con la regla de signos en la resta, el resultado será negativo. Así que, -8 - 4 = -12.

Es importante mencionar que la regla de signos en la suma y resta también se aplica cuando trabajamos con más de dos números. Por ejemplo, si tenemos 5 + (-2) + (-6), podemos agrupar los números con el mismo signo y luego sumarlos. En este caso, el resultado sería 5 + (-2) + (-6) = -3.

En resumen, la regla de signos en la suma y resta nos permite determinar el signo resultante al sumar o restar números con distintos signos. Si los números tienen el mismo signo, el resultado será positivo, mientras que si los números tienen signos opuestos, el resultado será negativo. Esta regla es fundamental para realizar operaciones matemáticas correctamente y comprender el comportamiento de los números en diferentes situaciones.

Cómo utilizar la regla de signos para simplificar expresiones algebraicas

Cómo utilizar la regla de signos para simplificar expresiones algebraicas

En el álgebra, las expresiones pueden volverse complicadas y difíciles de manejar. Sin embargo, existe una regla simple que nos ayuda a simplificar estas expresiones, conocida como la regla de signos. Esta regla nos permite determinar el signo resultante de una operación de suma o resta entre números con diferentes signos.

La regla de signos establece que si tenemos dos números con el mismo signo y los sumamos o restamos, el resultado será un número con el mismo signo. Por ejemplo, si tenemos dos números positivos y los sumamos, el resultado será positivo. Si tenemos dos números negativos y los restamos, el resultado también será negativo.

Por otro lado, si tenemos dos números con signos opuestos y los sumamos o restamos, el resultado será un número con el signo del número de mayor valor absoluto. Por ejemplo, si tenemos un número positivo y un número negativo y los sumamos, el resultado será el número con el mayor valor absoluto y llevará el signo del número con mayor magnitud.

Para utilizar la regla de signos en la simplificación de expresiones algebraicas, simplemente debemos aplicarla a cada término de la expresión. Podemos agrupar los términos con el mismo signo y sumarlos o restarlos según corresponda. Luego, simplificamos la expresión combinando los términos resultantes.

En resumen, la regla de signos es una herramienta fundamental en el álgebra para simplificar expresiones. Nos permite determinar el signo resultante de una operación de suma o resta entre números con diferentes signos. Al aplicar esta regla a cada término de una expresión algebraica, podemos simplificarla y hacerla más manejable. ¡Utiliza la regla de signos para simplificar tus expresiones y facilitar tus cálculos algebraicos!

Tips y trucos para dominar la regla de signos en la suma y resta

La regla de signos en la suma y resta es una de las bases fundamentales en el álgebra y es importante dominarla para resolver problemas matemáticos de manera correcta. Aunque puede parecer complicada al principio, existen algunos tips y trucos que pueden facilitar su comprensión y aplicación.

El primer tip es recordar que dos números con el mismo signo se suman o restan para obtener un número con el mismo signo. Esto significa que si tenemos dos números positivos, su suma o resta también será positiva. Por otro lado, si tenemos dos números negativos, su resultado será negativo.

Por otro lado, si tenemos dos números con signos diferentes, la regla de signos establece que el resultado será el signo del número con mayor valor absoluto. Por ejemplo, si tenemos -5 + 3, el resultado será negativo ya que el número -5 tiene un valor absoluto mayor que el 3.

Otro truco útil es convertir los problemas de suma y resta en problemas de adición. En lugar de sumar o restar números con diferentes signos, podemos convertirlos en problemas de adición utilizando la regla de signos. Por ejemplo, en lugar de restar -7 - 4, podemos convertirlo en -7 + (-4) y resolverlo como una suma.

Finalmente, es importante recordar que los paréntesis pueden cambiar el signo del número. Si tenemos una expresión como -(3 + 5), podemos resolver primero la suma dentro de los paréntesis y luego cambiar el signo al resultado para obtener el resultado final.

Esto también te interesa...Producto escalar de dos vectores: Cálculo y propiedades en Matemáticas

---

¿Necesitas regularización académica?

No más complicaciones para aprender álgebra. Reserva tus sesiones llenando la forma siguiente y nos vemos en línea.

También te recomiendo la herramienta Math Solver para practicar una vez que hayas intentado resolver tus ejercicios.

Si quieres conocer otros artículos parecidos a Expresión algebraica. Aprende sobre las combinaciones de letras y números puedes visitar la categoría Álgebra.