Ejemplos resueltos: Cálculo de la distancia entre dos puntos
Para calcular la distancia que hay entre dos puntos ubicados en el plano cartesiano, ¿qué teorema se aplica o sirve para determinar ese valor?
Para calcular la distancia entre dos puntos en un plano cartesiano, utilizamos algo llamado "Teorema de Pitágoras". Imagina que tienes un plano cartesiano, que es como una gran cuadrícula con líneas horizontales y verticales. Ahora, coloca dos puntos en esa cuadrícula. Uno podría ser el punto donde está tu casa y el otro podría ser el punto donde está tu escuela, por ejemplo.
Ahora, imagina que dibujas un rectángulo invisible alrededor de esos dos puntos de manera que los puntos sean las esquinas opuestas del rectángulo. Este rectángulo tendrá dos lados que son líneas horizontales y dos lados que son líneas verticales. Estas líneas forman lo que llamamos "catetos" en matemáticas.
El "Teorema de Pitágoras" nos dice cómo encontrar la distancia más corta entre esos dos puntos, que es la línea diagonal que va desde una esquina del rectángulo a la otra. Esta línea diagonal se llama "hipotenusa".
Es como si estuvieras jugando a ser un detective matemático, usando pistas (las coordenadas x y y) para encontrar la respuesta al misterio (la distancia entre los dos puntos).
- Ejemplos resueltos: Cálculo de la distancia entre dos puntos
- Ejemplo resuelto: Calcula la distancia del punto C(4,-3) al punto D(2,5) del plano cartesiano.
- Más ejercicios de distancia entre dos puntos
- Ejemplo 3: Calcular la distancia entre los puntos E(0, 0) y F(0, 5).
- Otros ejemplos resueltos para el cálculo de la distancia entre dos puntos.
- ¿Llevas un curso de geometría analítica?
- Conclusión
- ¿Tienes preguntas o quieres saber más?
- Suscíbete al Niusleter
Ejemplos resueltos: Cálculo de la distancia entre dos puntos
La distancia entre dos puntos en el plano cartesiano es una medida de la longitud de la línea recta que conecta ambos puntos.
En las coordenadas cartesianas la distancia entre dos puntos se calcula utilizando la fórmula de distancia euclidiana, que es una expresión matemática que toma en cuenta las coordenadas de los puntos y la raíz cuadrada de la suma de los cuadrados de las diferencias entre ellas
En esta publicación encontrarás ejemplos y problemas de distancia entre dos puntos en el plano cartesiano que se resuelven con la aplicación directa de la fórmula de la distancia.
Las aplicaciones de la fórmula de la distancia entre dos puntos también se explican en un video, encuentra la liga al final de este art{iculo, donde encontrarás ejercicios resueltos de distancia entre dos puntos.
Recuerda que los problemas de distancia entre dos puntos cualesquiera, ubicados en el plano cartesiano, se atacan mediante la aplicación directa de la fórmula para la distancia.
Vamos a las coordenadas cartesianas para resolver un ejemplo de cálculo de la distancia entre dos puntos para clarificar el procedimiento paso a paso.
Ejemplo resuelto: Calcula la distancia del punto C(4,-3) al punto D(2,5) del plano cartesiano.
Paso 1. Aplicar la fórmula de la distancia entre dos puntos
¿Cuál es la fórmula para calcular la distancia entre dos puntos?. Recordemos que, para encontrar la distancia entre dos puntos en el plano cartesiano, debemos partir de la ecuación o fórmula de la distancia entre dos puntos que se muestra enseguida:
La fórmula para hallar la distancia se deduce a partir del teorema de pitágoras, donde la distancia entre los puntos de interés corresponde con la hipotenusa de un triángulo rectángulo que se complementa con el segmento horizontal y el segmento vertical que corresponden a los catetos.
Paso 2. Decidir cuáles son los puntos 1 y 2.
El siguiente paso es decidir cuál será nuestro Punto 1 y cuál nuestro Punto 2.
Es irrelevante cuál de los dos será el punto 1 y el punto 2, así que, para nuestro caso en particular usaré el punto C(4,-3) como punto 1 y el punto D(2,5) como el punto 2.
Una vez decidido lo anterior, nuestras coordenadas para encontrar la distancia entre los punto C y D son las siguientes:
Paso 3. Sustituir valores en la fórmula de la distancia entre dos puntos.
Enseguida debemos sustituir los valores de cada variable en su lugar correspondiente de acuerdo con la fórmula inicial:
Paso 4. Hacer operaciones.
Finalmente es el momento de aplicar la fórmula y hacer los cálculos finales:
Concluimos entonces, que la distancia entre los puntos C(4, -3) y D(2,5) es igual a la raíz cuadrada de 68.
Más ejercicios de distancia entre dos puntos
Ejemplo 1: Calcular la distancia entre los puntos A(2, 3) y B(5, 7).
Solución: Utilizando la fórmula de distancia euclidiana, tenemos:
d = √((x2 - x1)² + (y2 - y1)²)
Donde d es la distancia entre los puntos, x1 e y1 son las coordenadas del primer punto (A en este caso) y x2 e y2 son las coordenadas del segundo punto (B en este caso).
Sustituyendo los valores de los puntos A y B, tenemos:
d = √((5 - 2)² + (7 - 3)²) d = √(3² + 4²) d = √(9 + 16) d = √25 d = 5
Por lo tanto, la distancia entre los puntos A y B es de 5 unidades.
Ejemplo 2: Calcular la distancia entre los puntos C(-1, -2) y D(3, 4).
Solución: Utilizando la fórmula de distancia euclidiana, tenemos:
d = √((x2 - x1)² + (y2 - y1)²)
Sustituyendo los valores de los puntos C y D, tenemos:
d = √((3 - (-1))² + (4 - (-2))²) d = √(4² + 6²) d = √(16 + 36) d = √52 d ≈ 7.21
Por lo tanto, la distancia entre los puntos C y D es de aproximadamente 7.21 unidades.
Ejemplo 3: Calcular la distancia entre los puntos E(0, 0) y F(0, 5).
Solución: Utilizando la fórmula de distancia euclidiana, tenemos:
d = √((x2 - x1)² + (y2 - y1)²)
Sustituyendo los valores de los puntos E y F, tenemos:
d = √(0² + (5 - 0)²) d = √(0 + 25) d = √25 d = 5
Por lo tanto, la distancia entre los puntos E y F es de 5 unidades.
Otros ejemplos resueltos para el cálculo de la distancia entre dos puntos.
En mi canal de YouTube he colocado un video con ejemplos en los que resuelvo problemas de distancia entre dos puntos.
Para verlos sólo sigue la liga de la parte final de esta página.
En el canal puedes encontrar más ejemplos resueltos de distancia entre dos puntos, así como problemas resueltos de línea recta y otros temas de geometría analítica, y desde luego que tienes toda la explicación detallada de la metodología para resolver la distancia entre dos puntos con ejemplos.
Ver video tutorial con ejemplos resueltos para el cálculo de la distancia entre dos puntos
¿Llevas un curso de geometría analítica?
Entonces puede serte útila saber cómo identificar las cónicas con la ecuación general de segundo grado. Dale un vitazo al artículo y comenta cómo te va con él.
Conclusión
En conclusión, hemos repasado algunos ejemplos resueltos: cálculo de la distancia entre dos puntos en el plano cartesiano.
Dimensión que se puede calcular utilizando la fórmula de distancia euclidiana, la cual toma en cuenta las coordenadas de los puntos y la raíz cuadrada de la suma de los cuadrados de las diferencias entre ellas.
Es importante recordar que esta fórmula se puede utilizar para cualquier par de puntos en el plano cartesiano, independientemente de su posición o dirección.
¿Tienes preguntas o quieres saber más?
te invito a escribir tus preguntas sobre este tema. Usa la sección de comentarios al final de esta página y regresa prono para leer la respuesta a tu pregunta.
Si necesitas asesoría más detallada para calcular la distancia entre dos puntos y quieres hacer ejemplos con una guía paso a paso para resolverlos, entonces contrata tu sesión de regularización académica. Llena la forma siguiente y al enviarla recibirás todas las instrucciones en tu email. ¡Nos vemos pronto!
Suscíbete al Niusleter
Si tienes algún comentario o pregunta sobre cómo resolver problemas de distancia entre dos puntos, no dudes en hacerlos llegar desde la parte inferior de esta página o en la forma de contacto.
Aumento la rentabilidad de escuelas, colegios y universidades particulares.
Creación y posicionamiento de la marca personal docente.
- Explorando las características del prisma rectangular - mayo 9, 2024
- Descubre las características del heptágono - mayo 9, 2024
- El Marketing one to one para colegios - noviembre 14, 2023
Si quieres conocer otros artículos parecidos a Ejemplos resueltos: Cálculo de la distancia entre dos puntos puedes visitar la categoría Puntos en el plano cartesiano.
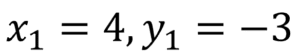
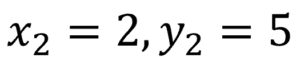
Deja un comentario