Producto Cruz: Definición, cálculo y aplicaciones
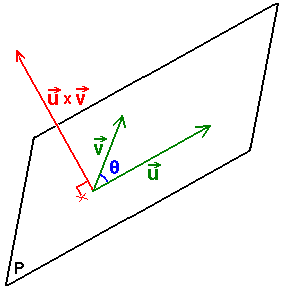
Producto Cruz. El producto cruz es una operación matemática que se utiliza en el ámbito de la geometría y la física. Se define como el resultado de multiplicar dos vectores y obtener un tercer vector perpendicular a ambos.
Su magnitud se calcula mediante el determinante de una matriz 3x3 y su dirección se determina utilizando la regla de la mano derecha. El producto cruz tiene aplicaciones en diversos campos, como la física y la astronomía, y es útil para calcular áreas de paralelogramos y triángulos.
Definición del producto cruz
Veamos primero la definición de producto cruz. El producto cruz es una operación matemática que se realiza entre dos vectores en el espacio tridimensional. El resultado de esta operación es un nuevo vector que está perpendicular a los dos vectores originales. El producto cruz es conocido también como producto vectorial.
Definición del Producto Vectorial: El producto vectorial, también conocido como producto cruz, es una operación entre dos vectores en un espacio tridimensional que resulta en un nuevo vector perpendicular al plano definido por los vectores originales. El producto vectorial se calcula utilizando determinantes y propiedades geométricas.
Propiedades del producto vectorial o producto cruz
El producto cruz de dos vectores paralelos es igual a un vector nulo.
El producto cruz es distributivo respecto a la suma de vectores.
El producto cruz no es conmutativo, es decir, el orden de los vectores afecta el resultado.
Magnitud del producto cruz
La magnitud del producto cruz es una medida de la longitud de un vector resultante del producto cruz entre dos vectores. El producto cruz es una operación vectorial que se utiliza para determinar un vector perpendicular a dos vectores dados. La magnitud del producto cruz proporciona información sobre la fuerza y la dirección del vector resultante.
Para calcular la magnitud del producto cruz, se utiliza la fórmula ||A × B|| = ||A|| ||B|| sen(θ), donde ||A × B|| representa la magnitud del producto cruz de los vectores A y B, ||A|| y ||B|| son las magnitudes de los vectores A y B, y θ es el ángulo formado entre los dos vectores.
La magnitud del producto cruz se expresa en unidades de longitud. Es importante tener en cuenta que la magnitud del producto cruz es siempre un valor positivo, ya que representa la longitud del vector resultante sin tener en cuenta la dirección. Además, cuanto mayor sea la magnitud del producto cruz, mayor será la fuerza resultante del vector.
La magnitud del producto cruz tiene diversas aplicaciones en física y matemáticas. En física, se utiliza para calcular el momento angular de un objeto en movimiento, así como para determinar la fuerza magnética que actúa sobre una partícula cargada en un campo magnético. En matemáticas, se utiliza para determinar el área de un paralelogramo formado por dos vectores y para resolver ecuaciones paramétricas en el espacio tridimensional.
Propiedades del producto cruz
El producto cruz es una operación matemática que se aplica exclusivamente a vectores en un espacio tridimensional. Este producto da como resultado un nuevo vector, perpendicular al plano formado por los dos vectores originales. Es una herramienta fundamental en geometría y física, ya que permite calcular áreas, volúmenes y momentos. Además, es útil para determinar la direccionalidad de fuerzas y momentos en sistemas físicos.
Una de las propiedades más importantes del producto cruz es que el resultado es un vector perpendicular al plano formado por los dos vectores originales. Esto significa que si tenemos dos vectores A y B, su producto cruz A×B será un vector C perpendicular a ambos. Esta propiedad es muy útil para determinar la dirección y sentido de fuerzas y momentos en un sistema, ya que nos indica cómo actúa una fuerza en relación a un objeto.
Esto también te interesa...
Producto escalar de dos vectores: Cálculo y propiedades en MatemáticasOtra propiedad relevante del producto cruz es que su magnitud está relacionada con el área del paralelogramo formado por los dos vectores originales. En otras palabras, si tenemos dos vectores A y B, el módulo del producto cruz A×B será igual al área del paralelogramo formado por A y B. Esta propiedad es muy útil en geometría para calcular áreas de figuras planas, así como para determinar el momento de inercia de objetos en física.
Además de estas propiedades, el producto cruz también cumple con la propiedad distributiva respecto a la suma de vectores. Esto significa que si tenemos tres vectores A, B y C, podemos distribuir el producto cruz de A y (B + C) como el producto cruz de A y B más el producto cruz de A y C. Esta propiedad es útil para simplificar cálculos y resolver problemas más complejos que involucren varias fuerzas o momentos.
En resumen, el producto cruz es una operación matemática que permite obtener un nuevo vector perpendicular al plano formado por dos vectores originales. Este vector resultante tiene propiedades únicas, como ser proporcional al área del paralelogramo formado por los vectores originales. Además, cumple con la propiedad distributiva respecto a la suma de vectores. Estas propiedades hacen del producto cruz una herramienta fundamental en geometría y física, con diversas aplicaciones en el cálculo de áreas, volúmenes y momentos.
Para calcular el producto vectorial
Cálculo del módulo del producto cruz
El módulo del producto cruz se puede calcular utilizando un determinante de dimensión 3x3. Este determinante se forma utilizando las coordenadas de los vectores originales y su resultado representa el área de un paralelogramo en el espacio generado por esos vectores.
Dirección del producto cruz y regla de la mano derecha
La dirección del vector resultado del producto cruz se determina utilizando la regla de la mano derecha. Esta regla establece que si curvamos los dedos de la mano derecha desde el primer vector hacia el segundo, el vector resultado apunta en la dirección en la que se extiende el dedo pulgar. De esta manera, podemos visualizar fácilmente la dirección del producto cruz.
El producto cruz en el espacio tridimensional
El producto cruz es una operación esencial en el ámbito del espacio tridimensional. Permite calcular un nuevo vector que es perpendicular a los dos vectores originales. Este cálculo se realiza utilizando matrices de dimensiones 3x3.
Cálculo del producto cruz utilizando matrices
Para calcular el producto cruz de dos vectores en el espacio tridimensional, se utiliza una matriz especial:
- La primera fila contiene los coeficientes del vector unitario en la dirección del eje x.
- La segunda fila contiene los coeficientes del vector unitario en la dirección del eje y.
- La tercera fila contiene los coeficientes del vector unitario en la dirección del eje z.
Para obtener el resultado del producto cruz, se deben multiplicar los vectores originales por esta matriz y realizar las operaciones correspondientes.
Aplicaciones del producto cruz en Física y Astronomía
El producto cruz tiene numerosas aplicaciones en distintos campos, especialmente en Física y Astronomía. Algunas de ellas son:
- Cálculo del par de fuerzas sobre un objeto en rotación.
- Determinación de la fuerza magnética experimentada por una carga en movimiento en un campo magnético.
- Análisis de la trayectoria de partículas cargadas en campos magnéticos.
Estas aplicaciones demuestran la importancia del producto cruz en el estudio de fenómenos físicos y astronómicos en el espacio tridimensional.
Cálculo del área de un paralelogramo utilizando el producto cruz
El cálculo del área de un paralelogramo es una aplicación directa del producto cruz. Para calcular el área, se utilizan los vectores que forman los lados del paralelogramo. La fórmula para calcular el área utilizando el producto cruz es la siguiente:
Fórmula para calcular el área de un paralelogramo
- Sea A el primer vector del paralelogramo y B el segundo vector.
- Calculamos el producto cruz de A y B y obtenemos un nuevo vector C.
- La magnitud de C representa el área del paralelogramo.
El cálculo del área de un paralelogramo nos permite determinar la superficie que este ocupa en el espacio tridimensional. Es una herramienta fundamental en geometría y física, ya que se utiliza para calcular áreas en objetos con forma de paralelogramo, como por ejemplo, placas o superficies inclinadas.
Ejemplos y problemas resueltos
A continuación, se presentarán algunos ejemplos para ilustrar el cálculo del área de un paralelogramo utilizando el producto cruz:
Esto también te interesa...
Media, mediana y moda: Medidas de tendencia centralEjemplo 1:
Dados los vectores A = (2, 3, 1) y B = (4, 1, 5), calculemos el área del paralelogramo formado por estos vectores.
- Calculamos el producto cruz de A y B: C = (14, 6, -10)
- La magnitud de C es sqrt(332), por lo que el área del paralelogramo es sqrt(332).
Ejemplo 2:
Dados los vectores A = (3, 2, 4) y B = (1, 5, 2), calculemos el área del paralelogramo formado por estos vectores.
- Calculamos el producto cruz de A y B: C = (-18, 10, 13)
- La magnitud de C es sqrt(453), por lo que el área del paralelogramo es sqrt(453).
Estos ejemplos muestran cómo utilizar la fórmula del producto cruz para calcular el área de un paralelogramo. Es importante recordar que el resultado obtenido representa el área exacta del paralelogramo en unidades cuadradas.
Cálculo del área de un triángulo utilizando el producto cruz
Fórmula para calcular el área de un triángulo
El producto cruz también nos permite calcular el área de un triángulo. La fórmula para calcular el área de un triángulo utilizando el producto cruz es:
- Dados dos vectores a y b que representan dos lados del triángulo, el área del triángulo se calcula como la mitad del módulo del producto cruz entre los vectores a y b.
- Matemáticamente, podemos expresar esta fórmula como:
Área del triángulo = |(a x b) / 2|
Ejemplos resueltos de producto vectorial o producto cruz
A continuación se presentan algunos ejemplos y ejercicios resueltos para comprender mejor cómo calcular el área de un triángulo utilizando el producto cruz:
- Supongamos que tenemos los vectores a = (3, 1, 2) y b = (2, 4, 1) que representan dos lados del triángulo. Para calcular el área, hacemos el producto cruz entre los vectores:
(a x b) = ((1)(1) - (4)(2), (2)(2) - (3)(1), (3)(4) - (2)(1)) = (-7, 3, 10)
- Luego, calculamos el módulo del producto cruz:
|(a x b)| = sqrt((-7)^2 + 3^2 + 10^2) = sqrt(148) ≈ 12.16
- Finalmente, aplicamos la fórmula del área del triángulo:
Área del triángulo = |(-7, 3, 10) / 2| ≈ 12.16 / 2 = 6.08
Por lo tanto, el área del triángulo formado por los vectores a y b es aproximadamente 6.08 unidades cuadradas.
Continuando con esta metodología, podemos calcular el área de otros triángulos utilizando el producto cruz y aplicando la fórmula correspondiente.
área de un paralelogramo con vectores
Esto también te interesa...
Cómo identificar el grado de una ecuación: Guía práctica
Aumento la rentabilidad de escuelas, colegios y universidades particulares.
Creación y posicionamiento de la marca personal docente.
- Implementación de CRM en Instituciones Educativas: Optimizando la Gestión Académica - septiembre 24, 2024
- Comunicación con la Comunidad de Educación: Estrategias Efectivas para el Éxito Escolar - septiembre 17, 2024
- De prospecto a egresado, la importancia de hacer comunidad educativa: Forjando lazos duraderos en el entorno académico - septiembre 10, 2024
Si quieres conocer otros artículos parecidos a Producto Cruz: Definición, cálculo y aplicaciones puedes visitar la categoría Matemáticas.
-
Sara Giménez dice: Me ha llamado la atención la parte de las aplicaciones del producto cruz en Física y Astronomía. ¿Podrías profundizar un poco más sobre cómo se utiliza exactamente en esos campos, Sergio Ruiz?
-
Carlos Martín dice:
En física, el producto cruz se usa mucho para calcular momentos de fuerza y en electromagnetismo para determinar la dirección de la fuerza en un campo magnético. ¡Es super útil!
-
-
Sergio Ruiz dice:
Hola Lucía.
No es complicado entender el producto cruz. Lo que debemos hacer es practicar. Si lo haces, poco a poco tendrás más confianza y el conocimiento se anidará en tu cerebro.
Te invito a que me hagas llegar un mensaje desde la página de contacto para mandarte algunos ejercicios y explicación sobre este tema.
Gracias por comentar.
Saludos
Sergio Ruiz
-
-
-
Carlos Jiménez dice:
Oye, alguien sabe como usar la regla de la mano derecha para el producto cruz? siempre me lio con eso. Sergio Ruiz, en tu artículo dices que es importante, pero no me queda claro el método. Alguien ayuda?
-
Marta Vila dice:
Hola Carlos, la regla de la mano derecha se usa apuntando tu pulgar hacia el primer vector, el índice hacia el segundo y tu dedo medio te indicará la dirección del producto cruz. Practica un poco y seguro que lo consigues.
-
-
Manu G. dice:
Si el producto cruz sirve para calcular áreas, yo lo usaría para calcular el área de mi habitación así tengo excusa para no ordenarla, diciendo que estoy estudiando jajaja.
-
Julia R. dice:
Realmente fascinante cómo el producto cruz tiene tantas aplicaciones en física y astronomía. Sergio, tu explicación sobre cómo calcular el momento angular es clara y directa. ¡Gracias!
-
Sergio Ruiz dice:
Hola Julia.
Es un gusto poder servirte.
Saludos y a tus órdenes.
Sergio Ruiz
-
-
JavierL dice:
Es importante destacar que el producto cruz solo se define en tres dimensiones, algo que a veces se pasa por alto. Buen trabajo en incluir el cálculo mediante matrices, Sergio Ruiz.
-
AnaM dice:
estoy un poco confundida con la regla de la mano derecha, ¿alguien puede explicarmelo como si tuviera 5 años? nunca me acuerdo si es el pulgar o el índice el que va con la fuerza.
-
Ana María Monroy dice:
Me pregunto si hay algún truco para que los niños entiendan mejor el producto cruz, Sergio Ruiz menciona la regla de la mano derecha pero mi hijo sigue sin entender. ¿Alguna sugerencia?
-
Luis F dice:
Ana, intenta usar modelos o dibujos para explicarlo. A veces verlo visualmente ayuda mucho a los niños a comprender mejor estos conceptos.
-
Sergio Ruiz dice:
Hola Ana María.
Este es un tema que regularmente se aprende en el bachillerato, no sé si cuando dices "niños" te refieres a adolescentes. Si son niños de primaria o secundaria es poco probable que lo entiendan, no por ellos sino porque hay herramientas matemáticas que no han aprdndido en ese grado.
Si necesitas ayuda mándame un mensaje desde la página de contacto.
Gracias por comentar
Sergio Ruiz
-
-
Diego S dice:
Interesante artículo, Sergio Ruiz, pero creo que hay aspectos del producto cruz que podrían explicarse con mayor profundidad, especialmente en lo que respecta a sus aplicaciones en ingeniería y diseño. Por ejemplo, cómo afecta el diseño de estructuras o vehículos. ¿Alguien más piensa que deberíamos profundizar más en estos temas?
-
Pepe Juárez dice:
Me encanta ver artículos como este para ayudar a mis hijos con sus deberes de mate, aunque a veces creo que yo aprendo más que ellos. Buena explicación del producto cruz.
-
Teresa P dice:
Vaya, nunca pensé que volvería a encontrar el producto cruz interesante. Esto me hace querer desempolvar mis viejos libros de texto y volver a aprender. Buen trabajo Sergio Ruiz, explicado de manera que incluso alguien como yo puede entender.
-
Irene Valle dice:
Siempre me he preguntado cómo estas cosas de las matemáticas se aplican en la vida real. Leyendo sobre el área de un paralelogramo por el producto cruz me da una idea. Interesante.
-
RobertoN dice:
Así que ahora estamos haciendo artículos enteros sobre matemáticas básicas, ¿eh? Espero que el próximo tema sea sobre cómo sumar dos más dos. Aunque, para ser justo, el artículo de Sergio Ruiz no está mal.
-
RocioP dice:
Sobre el cálculo del área de un triángulo usando el producto cruz, siempre he pensado que las matemáticas tienen una belleza escondida en su simplicidad y complejidad al mismo tiempo.
-
Isabel C. dice:
Estoy buscando métodos innovadores para enseñar el producto cruz a mis estudiantes de secundaria. Sergio Ruiz, tu artículo ofrece una perspectiva interesante, pero me gustaría saber si tienes o conoces recursos adicionales, como ejercicios interactivos o visualizaciones, que podrían hacer el concepto más accesible para los jóvenes.
-
Alvaro J. dice:
Creo que el artículo podría mejorar explicando más a fondo las limitaciones del producto cruz en espacios de más de tres dimensiones. No es tan directo y simple como podría parecer.
-
Luisa Méndez dice:
Este artículo es oro puro para quienes nos fascina entender el universo a través de la matemática. Gran trabajo en la sección de aplicaciones, Sergio. Me ha abierto los ojos a nuevas formas de ver las cosas.
Sara Giménez 
Sergio Ruiz Deja un comentario
Más artículos sobre este mismo tema