Fórmula para la distancia entre dos puntos
Fórmula de la distancia entre dos puntos
Fórmula para la distancia entre dos puntos explicada a detalle en el plano cartesiano y usando el teorema de Pitágoras.
En este post estamos haciendo una descripción paso a paso del sustento que hay detrás de la fórmula para encontrar la distancia entre dos puntos cualesquiera que están ubicados en el plano cartesiano.
Como veremos más adelante, la fórmula de la distancia entre dos puntos en el plano cartesiano está sustentada y se deriva a partir del Teorema de Pitágoras, por ello es muy importante tener bien sustentados los conocimientos de trigonometría.
Aquí puedes ver ejemplos resueltos de la distancia entre dos puntos.
Vamos al punto, bueno a los dos puntos...
Derivación de la fórmula de la distancia entre dos puntos en el plano cartesiano.
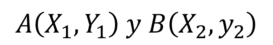
Para encontrar la distancia entre dos puntos en el plano cartesiano utilizaremos los puntos
Esto también te interesa...
Ejemplos resueltos: Cálculo de la distancia entre dos puntosFigura 1
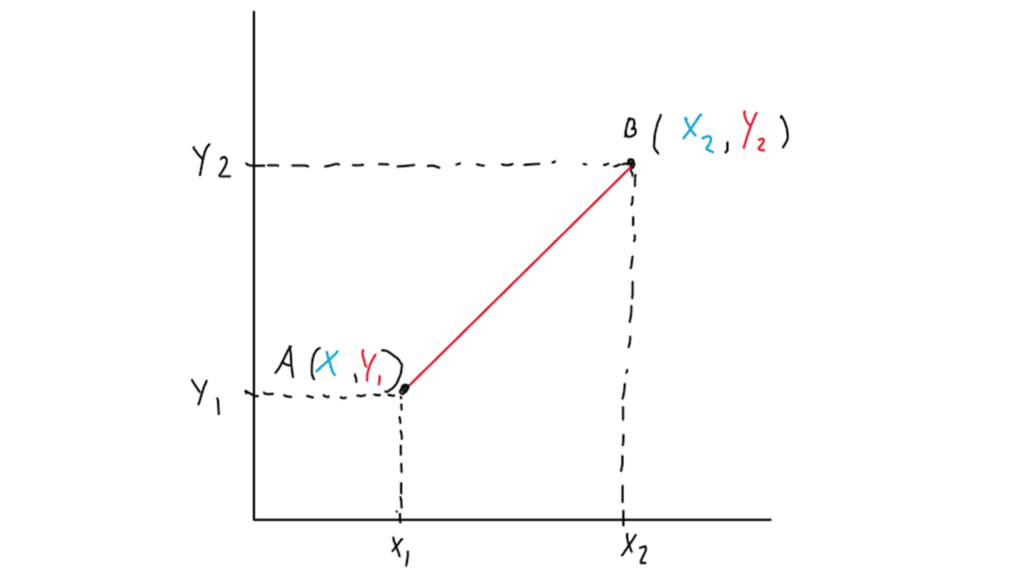
Para derivar la fórmula haremos uso del teorema de Pitágoras mediante la creación de un triángulo imaginario como se muestra en la figura 2. En esta misma figura 2 encontramos que la distancia del segmento “a” es igual a:
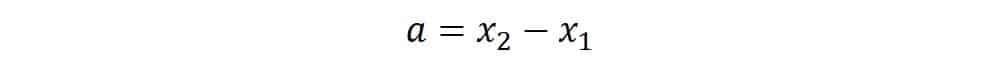
y de forma análoga la distancia del segmento “b” es igual a:
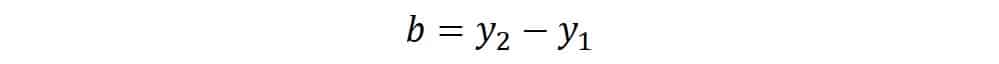
Figura 2
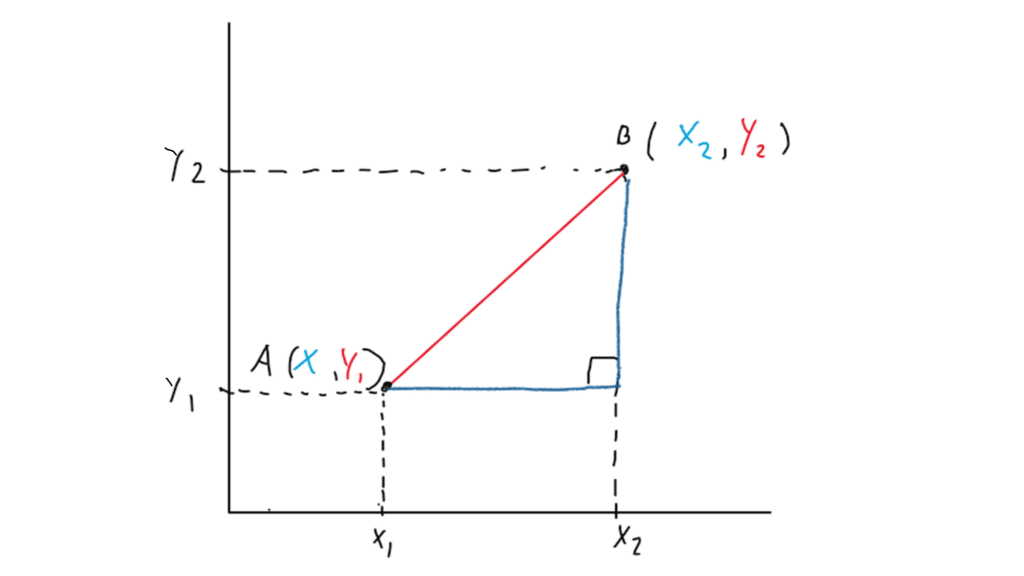
En este punto estamos en la posibilidad de aplicar al teorema de Pitágoras para encontrar la distancia del segmento AB.
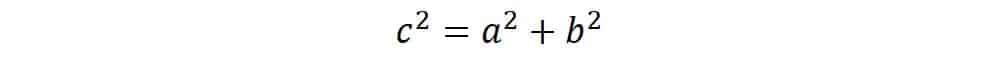
El teorema de Pitágoras está definido como sigue:
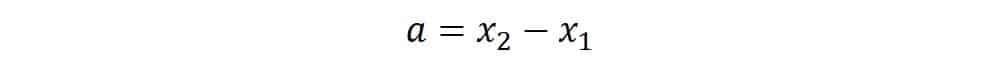
Y puesto que nosotros ya hemos definido que:
Esto también te interesa...
Ecuaciones de la recta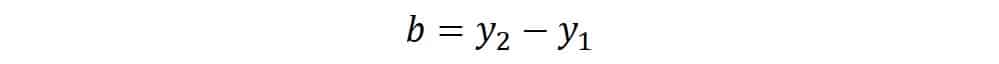y
Podemos utilizar estas dos definiciones, por lo que, sustituyendo términos tenemos la siguiente expresión:
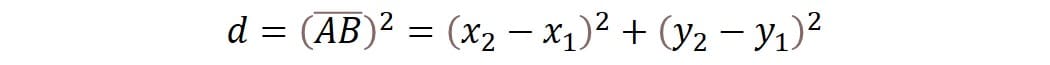
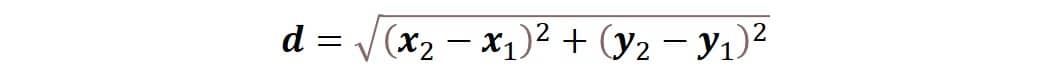
Finalmente, si queremos encontrar la distancia “d” del segmento AB, sólo debemos despejar para “d” y con ello tenemos la fórmula que para el cálculo de la distancia entre dos puntos en el plano cartesiano al que en algunos textos también se le refiere como la “longitud de un segmento de recta”, ambos términos son equivalentes.
La explicación dinámica de la obtención de esta fórmula se encuentra en el siguiente video:
Video tutorial que deduce la fórmula para calcular la distancia entre dos puntos en el plano cartesiano
¿Estás llevando un curso de Geometría Analítica?
Entonces puede serte útila saber cómo identificar las cónicas con la ecuación general de segundo grado. Dale un vitazo al artículo y comenta cómo te va con él.
Si tienes alguna duda o comentario sobre este tema o quieres hacer una aportación, puedes hacerlo en los comentarios de esta publicación o bien a través de la forma de contacto.
Suscríbete al Niusleter
Aumento la rentabilidad de escuelas, colegios y universidades particulares.
Creación y posicionamiento de la marca personal docente.
- Implementación de CRM en Instituciones Educativas: Optimizando la Gestión Académica - septiembre 24, 2024
- Comunicación con la Comunidad de Educación: Estrategias Efectivas para el Éxito Escolar - septiembre 17, 2024
- De prospecto a egresado, la importancia de hacer comunidad educativa: Forjando lazos duraderos en el entorno académico - septiembre 10, 2024
Si quieres conocer otros artículos parecidos a Fórmula para la distancia entre dos puntos puedes visitar la categoría Puntos en el plano cartesiano.
Deja un comentario